Constructing and Implementing a SAFI Portfolio

Innovations in efficiency, transparency, and technology have paved the way for systematic fixed income portfolios. In this paper, we discuss optimal portfolio construction, rebalancing, and implementation.

Systematic Active Fixed Income (SAFI) portfolio construction needs to manage multiple signals, continually steering the portfolio towards issuers with high alpha signal rankings and away from those with low rankings. At the same time, portfolio risk exposures, along other dimensions, need to be carefully controlled and unnecessary turnover avoided, particularly when rebalancing. Finally, execution capabilities are essential for implementing these strategies efficiently in the real world, given liquidity conditions, the availability of credit securities, and the market impact of trades.

Managing Multiple Signals

Systematic strategies follow a disciplined, quantitative approach to selecting risk exposures. They take a large number of small active risk exposures, such as selecting securities, issuers or sectors deemed attractive by the alpha signals. These intended exposures have the potential to contribute to excess returns, while carefully controlling risk in all other dimensions. Systematic security selection strategies are expected to track their benchmarks more closely than most fundamental active portfolios, with attractive risk-adjusted active performance.

Alpha signals, closely related to style factors, are a key input in systematic fixed income. Indeed, the decisions about which securities to buy or sell are determined based on signal scores that measure a security or issuer’s exposure to [un]desirable style factors at a given point in time.

To form a value factor, for example, this approach may start by calculating a signal that measures the extent to which a bond is over- or underpriced, relative to its peers, then use this analysis to construct a value factor by forming two portfolios: one with high-scoring bonds and one with low-scoring. The difference between the two portfolio returns captures the return on the value factor. Figure 1 illustrates this simple but intuitive methodology: Barclays QPS divides the investment universe (Bloomberg US Investment Grade Corporate Bond index) into quintile portfolios sorted by signal scores for value, momentum, and sentiment respectively. The evidence tells you that owning the top quintile and avoiding the bottom quintile would lead to outperformance. In other words, there’s alpha-generating potential within these signals.

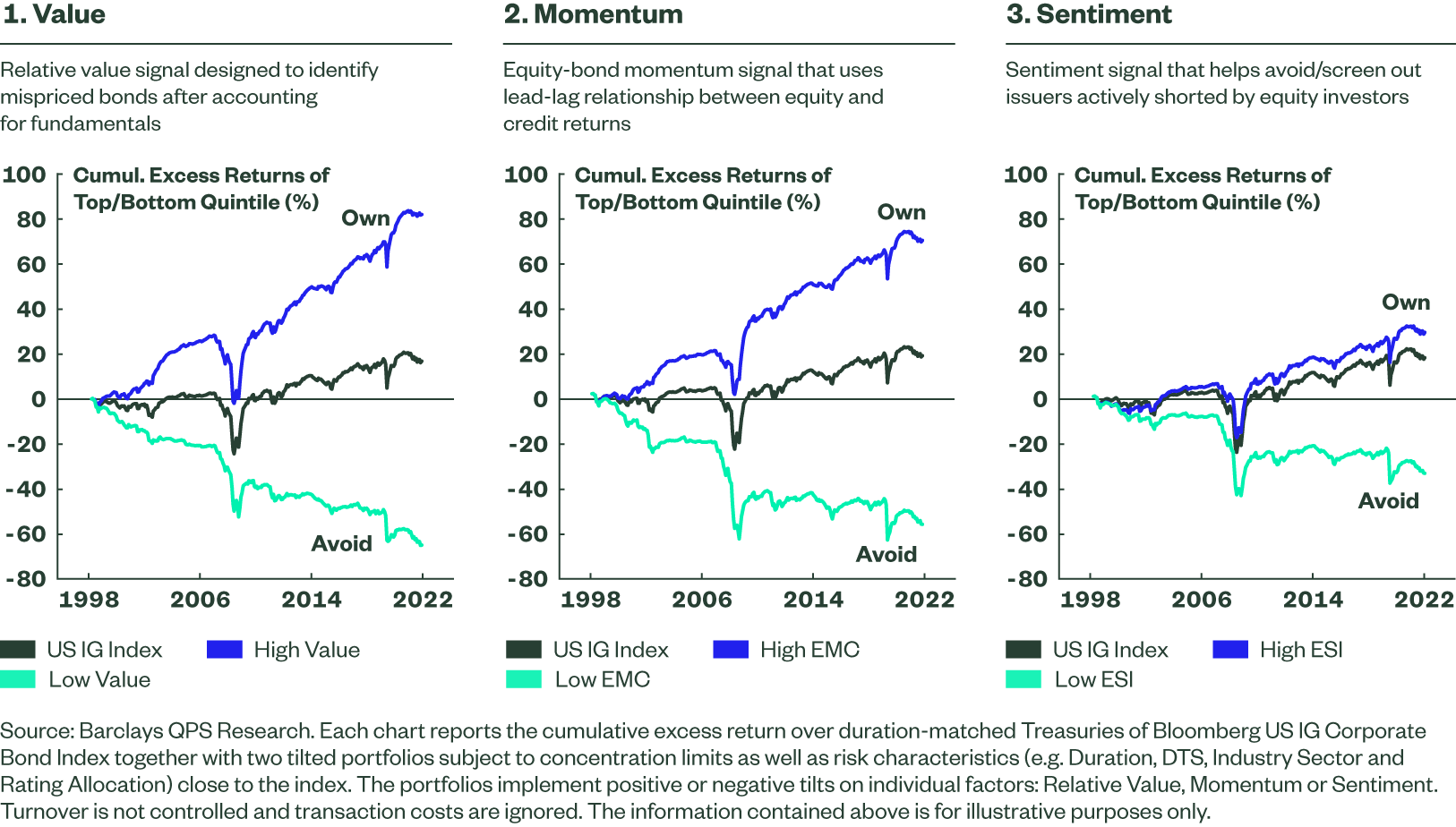
Given multiple signals, each of which could be used on its own to construct a portfolio that is expected to outperform the benchmark, what is the best way to build a portfolio that takes advantage of the information content in all of them?

Optimal Portfolio Construction

Once a number of efficacious signals have been identified, the next step is to use them to construct and maintain a portfolio. Defining the optimal portfolio is fairly straightforward: an optimization can identify the portfolio of securities that maximizes the signal score while satisfying all of the constraints on systematic and idiosyncratic risk. Then the universe of securities supplied as candidates for inclusion in the portfolio can be restricted to those with liquidity metrics above a certain threshold.

At this point, we run into a number of frictions that may not have been addressed in the first step of signal identification and evaluation. First, as we attempt to integrate different signals, we may find that they provide conflicting views on a particular issuer; we need to find the best way to make use of all available information. Is it better to form a separate portfolio based on each signal and then combine portfolios, or first to combine the signals and then form a single portfolio? How should we determine the weights assigned to different signals? We also need to take steps to limit transaction costs while still keeping the portfolio tilted to securities with high scores.

One possibility might be to diversify the portfolio by dividing the assets and running separate smaller portfolios, one based on each signal. However, this approach can lead to inefficiency. When signals point in different directions, one might end up being long the bond in one portfolio while shorting it in another. Even if positions are netted out before trading, such offsetting trades could negate the possibility of a net return improvement from positioning in that name. It is thus more efficient first to combine signals and construct a single portfolio with high combined scores.¹

Polbennikov, Desclée and Dubois² illustrate this result with an example based on a combination of value and momentum strategies. They found that a portfolio constructed to optimize a 50/50 blend of value and momentum signals achieved significantly better performance — in terms of average outperformance and information ratio — than a 50/50 blend of two portfolios that independently optimized each of the two signals on its own.

It is also important to understand the relationship between signal values and expected alpha. For some signals, this relationship may be nearly linear, while for others it may be highly non-linear. It may help performance to transform the signals before combining them such that a unit difference in one signal relates to the same advantage in expected alpha as a unit difference in another. Another important question is whether the signals to be combined should be given equal weights or not. It might be beneficial to give greater weight to signals that have been more efficient at alpha generation or to decrease the weight of signals that are highly correlated with others.

In any such approach based on historical performance, there is an additional question of whether these weights, once chosen, should remain fixed or be adjusted dynamically as new experience is accumulated. Dynamic updating can offer substantial benefits and can keep the overall strategy attuned to current market trends, but it can also be prone to overfitting.

Rebalancing Effectively

By evaluating a proposed strategy in a simulated portfolio backtest, one can solve for the optimal portfolio at the start of each month and find that it generates substantial outperformance over the benchmark on a steady basis. However, these optimal portfolios can be very different from one month to the next; turnover can be so high that active performance net of transaction costs is negative. To avoid this pitfall of “churning” the portfolio, the optimization process should recognize the prior month’s holdings as the starting point for each monthly rebalancing and include a mechanism for limiting turnover. Rebalancing transactions –which are necessary both for risk control and for maintaining positive tilts to our alpha factors – must be kept to the minimum amount necessary for achieving these goals.

The most straightforward way to limit portfolio rotation is to impose a constraint on the maximum allowed turnover in a given month, say 10%.

However, a fixed limit on turnover may not be the most efficient way to control transaction costs. Due to changes in the liquidity environment, and depending on which bonds are traded, a 10% turnover in the portfolio can result in much higher transaction costs in one month than another. It might be more appropriate to place the constraint directly on transaction costs. Furthermore, there might be some months in which it is crucial to make a trade – for example, when bonds outside the portfolio are viewed as much more attractive than the ones being held, or the signal for bonds currently in the portfolio turns strongly negative. In other months, the differences in signal values may be less dramatic (i.e. there’s lower dispersion in signal scores) and the improvement in expected performance resulting from trading is much lower.

It therefore makes sense to allow larger transactions when the need is greater or to evaluate every trade to see if the improvement in signal scores that it produces justifies the transaction cost. This can be accomplished by changing the setup of the optimization problem. Rather than finding the portfolio that maximizes signal scores subject to risk and turnover constraints, we can find the portfolio that maximizes a composite objective function that rewards high signal scores but penalizes for estimated transaction costs.

Ben Dor and Guan³ compared the performance of three different approaches to controlling transaction costs in credit portfolio construction: a constraint on turnover, a constraint on transaction costs, and an objective function that maximizes expected returns net of trading costs. They find that constraining estimated transaction costs gives better long-term performance than constraining turnover, and that incorporating transaction costs into the objective function can perform the best out of the three. However, both approaches require a more complicated estimation process than simply constraining turnover.

Delivering Efficient Implementation

Even after assembling all of the above machinery — signals, risk metrics, liquidity filters, accounting for transaction costs, signal combination methodology and the portfolio optimization process — there is one more step critical to the success of the strategy, namely implementation. The asset manager’s goal is to construct a portfolio of exposures that are risk-aligned and exhibit high sensitivity to the desired style factors. The optimization process provides proposed trades that can accomplish this, given its a priori estimates of bond pricing and liquidity. However, it is crucial to obtain factor exposure at a sufficiently low trading cost so as not to affect negatively the strategy’s performance potential.

To that end, buy-side traders aim to purchase securities at or below the expected price in the optimizer. That is easier said than done, especially in volatile markets. Today, portfolio managers and buy-side traders have an increasingly rich data set of bond-level liquidity metrics to work with, given the pricing transparency available with the growth in electronic trading. This information can help control and limit transaction costs, improving implementation efficiency so as to generate the expected return of the strategy more reliably than was previously possible. Such efficiency can now be achieved generally via the secondary market, but also opportunistically through the primary market. In each instance, the implementation program will target specific spread levels and transaction costs to build the desired exposure. Leading institutional trading desks that manage large volumes of granular trade flows throughout the day are particularly well positioned to capitalize on this pricing data, resulting in improved execution and more efficient implementation.

No matter how much care is taken in the design of the optimization process to propose executable trades, there are bound to be surprises at execution time: pricing and availability for some bonds may turn out to be very different than the pricing inputs used at the time of optimization. To meet this challenge, the portfolio construction process needs to allow for flexibility to substitute specific bonds in the model portfolio to best achieve the goals of the rebalancing transaction, given the prevailing market conditions.

After rebalancing, the actual portfolio may not exactly match the model portfolio proposed by the optimizer. However, an experienced asset manager with advanced portfolio construction capabilities can employ several techniques to alleviate implementation challenges and harness implementation alpha:

Executing at better levels than the conservative pricing estimates used in optimization.

The optimization framework should use a conservative estimate of transaction costs, such as Barclays LCS, which provide a single-dealer estimate of the bid-offer spread for each security. These estimates tend to be conservative (higher than actual transaction costs), as the bid-offer viewed by a large execution desk across multiple dealers will likely result in lower costs. Furthermore, with the proliferation of electronic trading and the availability of new trading protocols, finding the counterparty going in the opposite direction has never been easier. Advantageous execution levels can be achieved when buying directly from a bond owner or selling to a willing buyer, once one is found.

Incorporating insights from market flow dynamics into the construction process.

Sophisticated fixed income managers who manage a variety of large fixed income ETFs, enjoy real-time access to market flow dynamics and live pricing information. Often, market liquidity will coalesce around these ETF vehicles and be the first port of call when investors are looking to adjust market exposure, particularly when sentiment is changing. A manager can use this real-time access to execute on those bonds considered in the strategy. This transaction flow information provides a reference to the intraday direction of spreads and expected execution levels as these change with market conditions. These insights can then be used to exploit market liquidity as it arises, so as to reduce transaction costs in the continuous management of the strategy.

Monitoring spread levels and risk constraints in security watchlists.

Certain bonds may have high factor scores, but fall short of the necessary liquidity and spread requirements after transaction costs. Again, electronic trading enables managers to conduct continuous and anonymous surveillance of securities’ pricing levels and market trade activity. Moreover, watchlists can be set up to rapidly (or automatically) bid or offer bonds that have reached predetermined spread or price levels. It also facilitates the substitution of one high-scoring bond for another as their spread levels and liquidity costs change, to capture higher expected returns. By incorporating such quantitative trading and liquidity insights into the portfolio construction and maintenance process, a sophisticated manager can improve the efficiency and reliability of implementation outcomes in the ongoing management of systematic strategies.

Accessing primary markets.

The primary market premium is well known to fixed income investors; when new bonds come to market, they are priced attractively at a concession to the issuer’s spread in secondary trading. Managers can participate in primary issuance to benefit from this concession and gain a performance boost relative to existing bonds from the same issuer. Whereas new corporate bonds enter standard bond indices at the end of the month of issue, at prices obtained from secondary market trading, a strategy of systematically buying new issues at primary issuance can help a portfolio outperform its benchmark. The magnitude of concessions and, hence, the alpha they can generate, vary with market supply and demand.

A detailed study by Ben Dor and Xu⁴ demonstrates that for a passive portfolio of US IG corporates, the average annual alpha generated by systematic application of such a strategy was 5-25 basis points per year between 2007 and 2013. Therefore, it is worthwhile to ensure sufficient flexibility throughout the construction process to enable the manager to exploit this premium on issuers with high factor score that come to the primary market with a new bond deal.

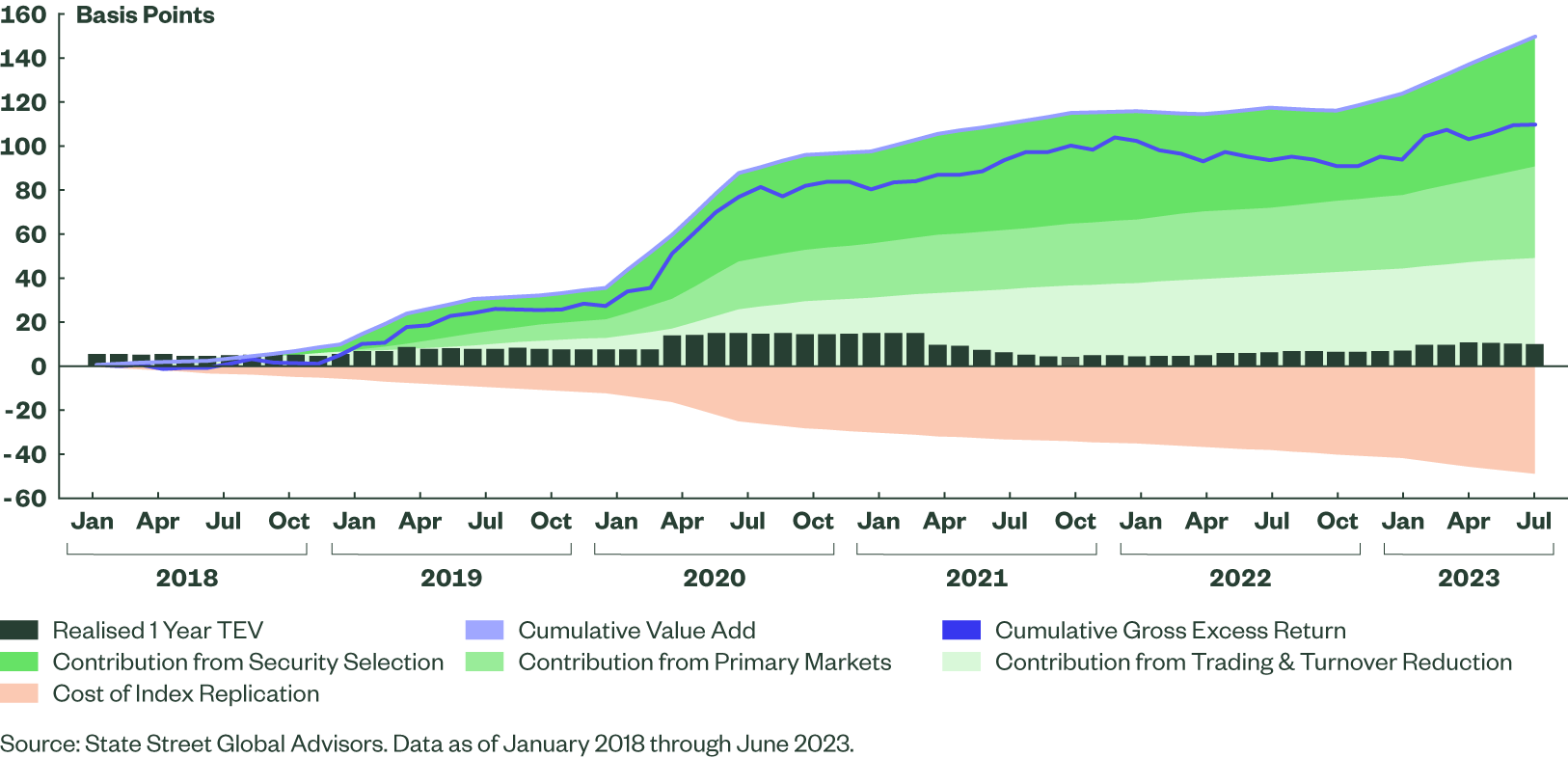
Figure 2 below demonstrates our skill in managing index fixed income portfolios, attributing the outperformance of a portfolio against its broad US investment grade credit benchmark to many of the methods for adding value discussed above. Over the five-and-a-half-year period shown, State Street Global Advisors has added a cumulative 149 bps of implementation alpha from a combination of trading and turnover reduction, participation in primary markets, and security selection.

Defined Benefit plans face a variety of economic and market challenges over their lifetimes and need to manage for those risks – from inflation and interest rates, to market performance and volatility. Unlike an idiosyncratic active approach, which looks at a relatively small number of issuers and makes subjective, high-conviction calls, a SAFI approach is systematically applied to every security in the investable credit universe. This provides a larger opportunity set, while staying within the desired risk limits and controlling tracking error.

More About SAFI

The data-driven insights in our Systematic Fixed Income strategies are informed by systematic signals delivered in the form of indices developed by the Barclays Quantitative Portfolio Strategy team, or QPS, which is well-recognized as an innovator in quantitative fixed income research. Their innovative signals and portfolio optimization methodologies form an important input to the process we, at State Street Global Advisors, use in the implementation and management of Systematic Active Fixed Income strategies.

Explore the State Street Global Advisors thought leadership series on Systematic Active Fixed Income investing to learn more about this innovative investment approach and its benefits.